
오일러 공식은 복소수를 삼각함수 또는 그 반대로 표현하는데 매우 유용한 공식이다.

다음과 같은 식으로 표현할 수 있다. e는 자연로그의 밑 상수, i는 허수단위 값, 그리고 삼각함수(cos, sin)로 이러우져 있다.
증명
다음은 테일러 급수를 이용한 방법이다.

테일러 급수에 따라서 위 식이 성립한다. 이에 따라 아래의 식들 또한 성립하게 되고


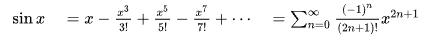
x가 복소수일 때, 무한급수를 각각의 함수로 정의할 수 있다.

오일러 등식

지수함수와 삼각함수가 연결되는 복소수 체계에서 위 공식에서 x에 π를 대입하면
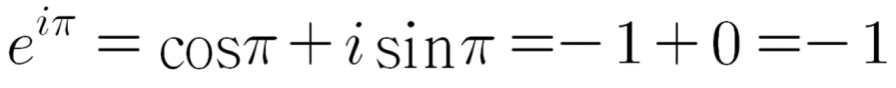
위와 식이 나타나며 양변에 1을 더하게 되면

다음과 같은 오일러 등식이 만들어진다.
참고
https://ko.wikipedia.org/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC_%EA%B3%B5%EC%8B%9D
오일러 공식 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. z = cos x + i sin x {\displaystyle z=\cos x+i\sin x} 는 복소평면에서 단위원을 뜻한다. 오일러 공식(Euler's formula)은 수학자 레온하르트 오일러의 이름이 붙은 공식이
ko.wikipedia.org
https://www.youtube.com/watch?v=LC3EAxXwyPQ&t=212s
'수학' 카테고리의 다른 글
| 굴절벡터 (0) | 2024.06.02 |
|---|---|
| 사원수 (0) | 2024.05.14 |
| 복소수 (0) | 2024.05.12 |
| 이원수(dual number) (0) | 2024.05.11 |
| 허수(Imaginary Number) (0) | 2024.05.09 |


